Algorithmic Mathematical Art
Here is an introduction and survey of Algorithmic Mathematical Art.
In the early 1990s, they were merely visualization aids in the study of mathematics. Gradually, the complexity and artistry of the images becomes an end itself.
Here, i examine the various methods of algorithmic mathematical art, and indicate the states of the art and possibilities. At the end, i give a definition of Algorithmic Mathematical Art.
Geometric Surfaces

max = 5; ContourPlot3D[ Sin[x*y] + Sin[y*z] + Sin[z*x] == 0, {x, -max, max}, {y, -max, max}, {z, -max, max}, Boxed -> False, Axes -> False, Mesh -> None, ContourStyle -> Directive[RandomColor[], Opacity[0.5], Specularity[ 1, 20]]]
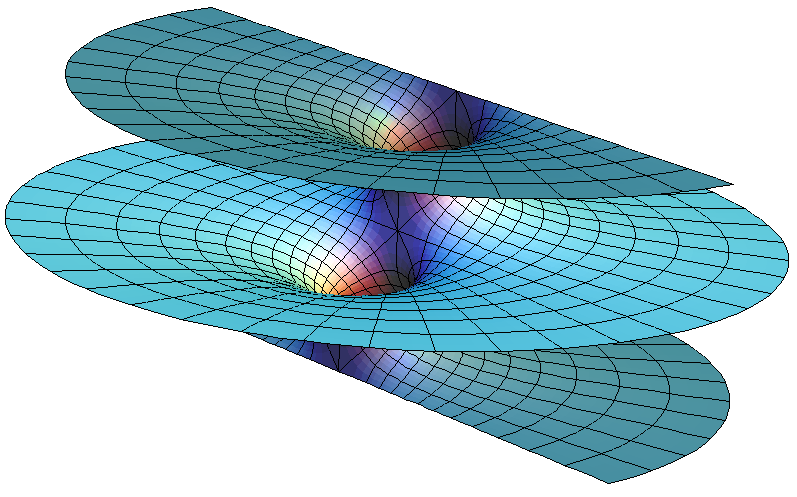
- Plots of arbitrary 3D surfaces for visual arts purposes has not been explored much.
- The exception is visualization of some special mathematical surfaces, especially in differential geometry. (e.g. minimal surfaces at http://virtualmathmuseum.org/Surface/gallery_m.html .)
- It is not much seen of arbitrary surfaces of equation of 3 variables.
- Equations with more than 3 variables can be projected or sliced to 3 dimensional space, and this is not much unexplored.
Regular Solids of 3 or more dimensions

- In 2 dimensions we have regular polygons, such as square and pentagon and hexagon.
- The 3-dimensional version is called regular polyhedron. e.g. cube, octahedron, icosahedron.
- The general name for such objects in any dimension is called polytope.
- Polyhedrons as artistic themes have been explored greatly, way back in the Greek times and in different cultures, often exhibited as toys, sculptures, paper models (origami), or hanging decoration.
- In modern times, polyhedrons have been exhibited as architecture element as well. e.g. Geodesic Domes

- Computer models as visual arts have been very popular.
- However, most of them are direct rendering of the mathematical object with almost no artistic value.
- Commonly seen are polyhedrons rendered with latest ray-tracing computer graphics advances, with some stellation or truncation.
- Highly artist algorithmic exploration of polytopes is almost non-existent.
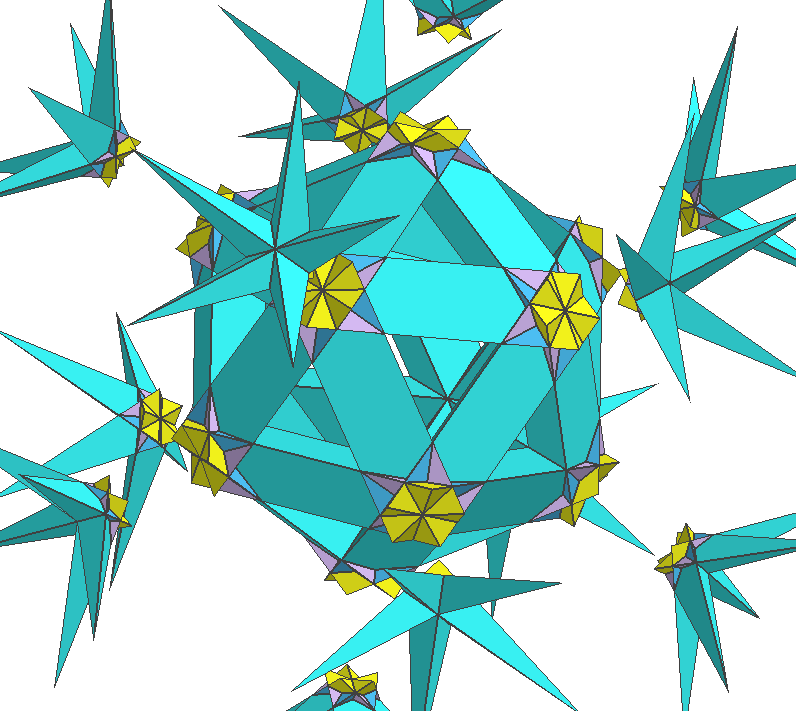
- The image by Michael Trott above, of a dodecahedron rendered as linked pentagonal rings, is a basic artistic exploration.
- For some examples of artistic algorithmic exploration, one can systematically examine ways to render a space by linked rings.
- For the centrally symmetric dodacahedron, for example, by some cleverness in linking, the links can extend to infinity as to fill the whole space with these links, and a cut-away view can be made to result in a artistic image.
- Or, polygonal tubes can be made to have larger radius, so that each polygonal “side” of the tube is a large flat area that a Maze can be incribed upon.
- The number of sides of the ring can increase or decrease according to certain parameters, such as symmetry location or distance from origin.
- Or, one can use spheres instead of rings.
- The coloring of balls around the dodecahedron can be exploited systematically, so to result in different symmetry groups of different groups of balls.
- Imagine a 3-D space with a cluster of differently colored balls that exhibits subtly different symmetry groups as in an elaborate intricate tiling work.
- Or, imagine 3-D space tiled uniformly by regular polyhedrons, with some walls open, as to form a 3-dimensional maze.
- If well done, a cut-away view or translucent view of this would be fantastic.
- A walk-thru as implemented in video games also has great potential.
- Solid stacks of cubes is called Polycube (a 3-dimensional version of polymino).
- Solid block sculptures with other regular polyhedron are basically unexplored.
- Block of connected tetrahedron are particularly interesting.
Plane Curves
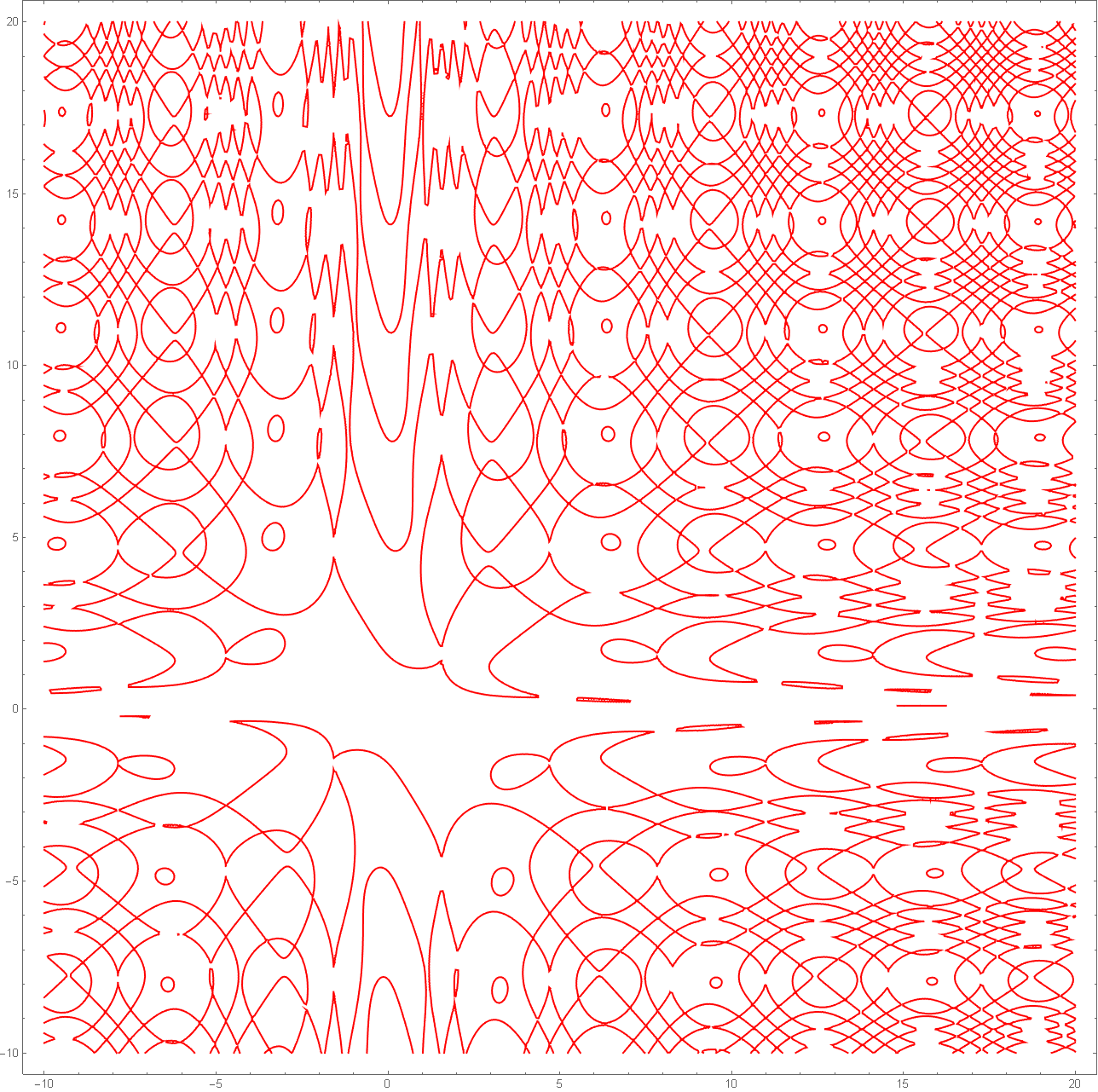
plots of the equation
ContourPlot[ Sin[x*Sin[y]] - Cos[y*Cos[x]] == 0, {x, -10, 20}, {y, -10, 20}, PlotPoints -> 50, ColorFunction -> Hue]
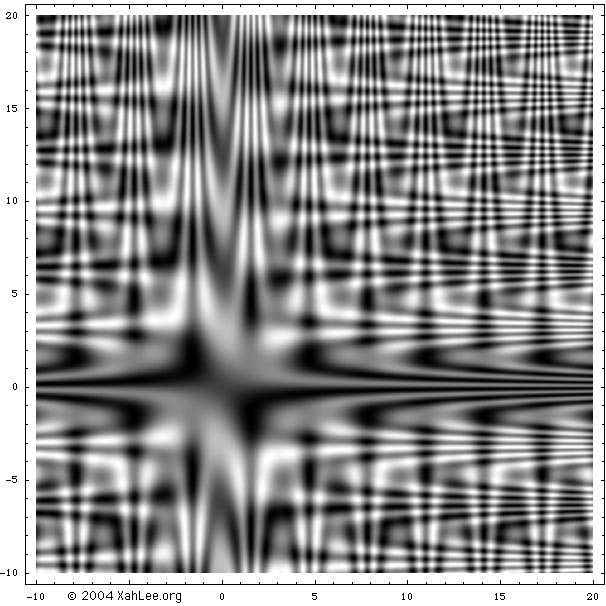
Two-dimensional plots for visual art purposes have not been explored much. Algebraic curves of more than 4 degrees are almost unexplored. One could create a program that systematically generates and plots all possible equations by degree or type, including non-algebraic ones.
Almost all ornamental elements in architecture or interior decorations are based in geometry, and most of them based on curves. Examples of curve based traditional art include: dome, arch, vault (based on arcs of circle), volutes (as scrolls on columns or violins) (based on various spirals), curlicue (based on Cornu spiral, lituus), toy Spirograph (based on roses, cycloidal curves).
Methods of artwork based on curves can include: tangents, envelope, caustics (String art); osculating circles and inversion, evolute/involute, pedal curves, parallel curves, pursuit curves.
Plane Geometry and Processes
Inversion of nested circles can result in many esthetic images.
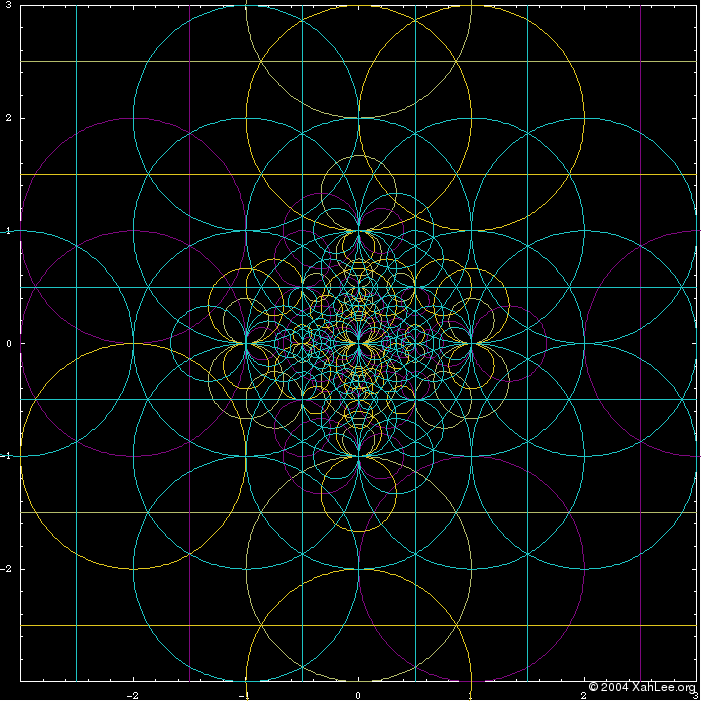


Geometric inversion can be used as a basis to create other patterns in the plane.
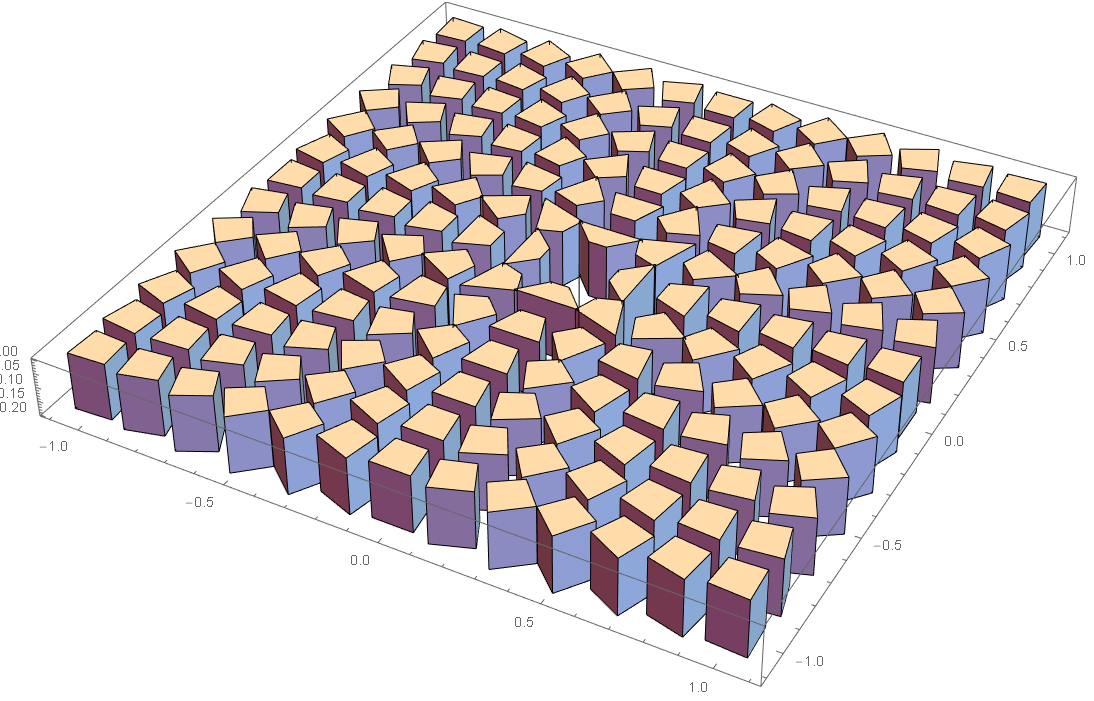
Geometric inversion applies to 3D, and higher dimensions.


- Traditional artworks based on geometric process include that of circles of tangency ( Appollonius circles ), various plane transformations applied to a grid or regular tilings (linear, affine, projective, geometric inversion, mobiüs transformation, stereographic projection, etc).
- A particular example in recreation is anamorphosis, which is a drawing that is not recognizable until its reflection is viewed on a shiny cylinder or metal ball. (e.g. Visual Arts: Trash Reflection)

For some images of traditional geometric processes, see:
- Circle Inversion Gallery
- Geometry: Transformation of the Plane
- Geometry: Transformation of the Plane II
- Stereographic Projection
- Anamorphic Projections (1989). By Paul Bourke. @
http://paulbourke.net/geometry/distort/
L-Systems, Turtle Graphics


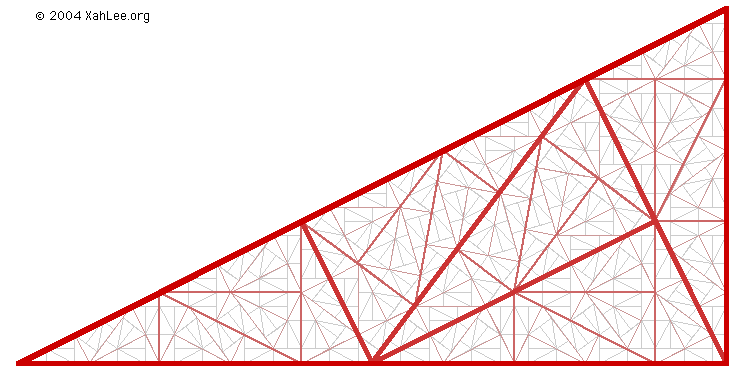

L-System is a recursive symbol-sequence replacement system originally devised to model plant growth. It is often used to generate self-similar images by interpreting the symbol-sequence as drawing commands or geometric objects. Turtle Graphics is from the programing language Logo, which algorithmically controls the movement of a pen, by specifying directions and pen down or up.
L-System and Turtle Graphics have been somewhat popular among recreational programers. However, there have not been serious studies of visual art possibilities with these methods. Commonly found are illustration of famous plane-filling curves in mathematics, plant-growth modeling, or simplistic symmetric drawings for children as a demo of Logo. Few of them are ingenious.
- Two-dimensional L-systems
- By Robert M Dickau.
- http://robertdickau.com/lsys2d.html
Plotting of Functions and Processes
Many functions in mathematics can be visualized as a plot. For curves and surfaces, the plotting scheme is simple. Often just on a 2D grid or 3D grid, with marked axes as coordinate. For other functions, such as vector valued functions, complex valued functions, mathematicians have developed other schemes to visualize these functions. Here are some examples.
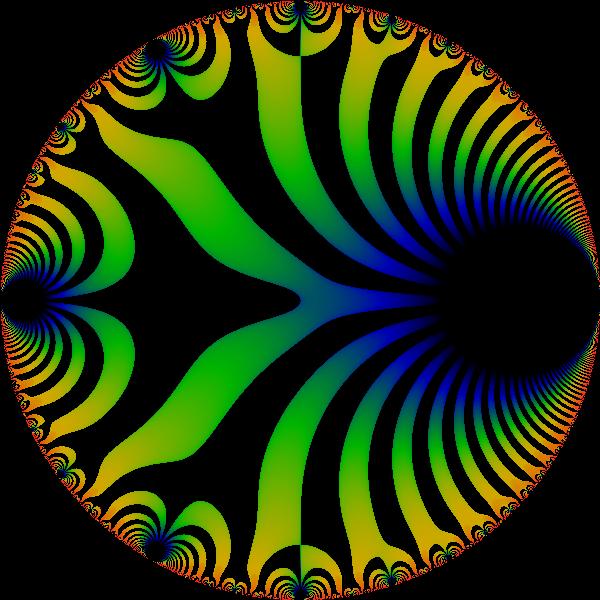
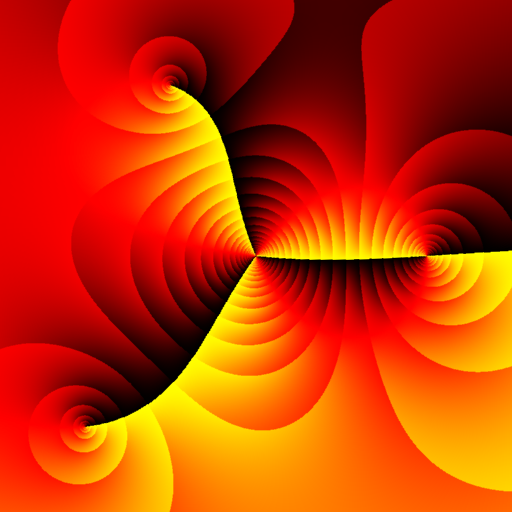
Tilings and Patterns


The main attraction of Celtic knot patterns is their geometric design, but the topological aspect (the “knot”) is also interesting mathematically. One can survey traditional designs to see whether they are really knots, or braids of how many strands, and how they are knotted. I'm not sure this has been studied much. There is little systematic study of algorithmic knot/weaving-pattern generations. (There have been systematic mathematical studies of weavings/fabrics by B Grünbaum and G C Shephard).
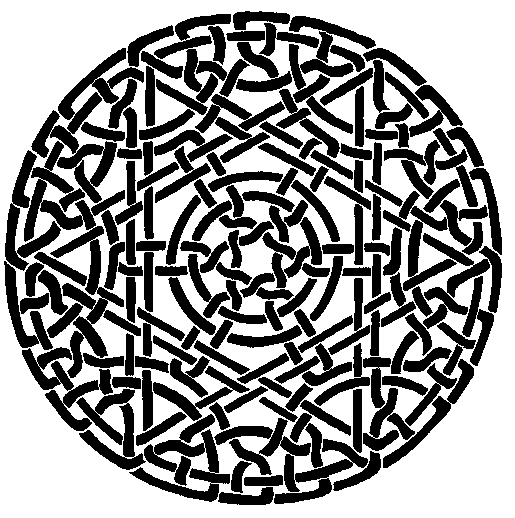
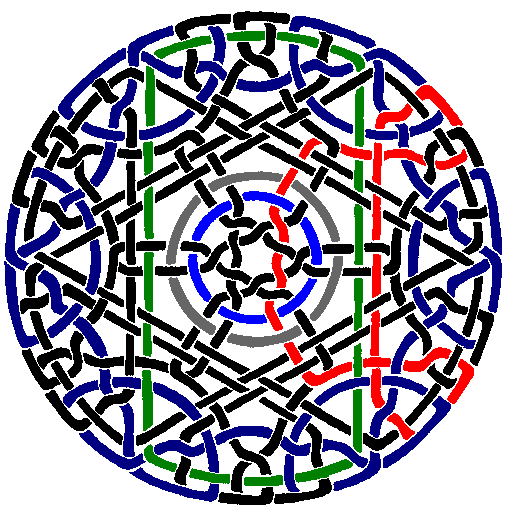







- There are many varieties of pattern designs by different cultures.
- The decorative Celtic knots and Islamic geometric tilings are particularly mathematical.
- Although there are great number of existing designs throughout the world and history, but with respect to mathematical or algorithmic classifications, there are not many varieties.
- This is not surprising when we consider that these artistic patterns are developed culturally by artisans, not as a result of mathematical analysis of plane symmetry or systematic algorithmic exploration.
- For plane patterns, it is known since the last century that there are 17 types of symmetries.
- According to Branko Grünbaum et al [Symmetry in Moorish and Other Ornaments, Comp. and Maths. with appls., Vol. 12B, Nos. 3/4. pp. 641-653, 1986], not all types are found in Alhambra, contrary to popular belief.
- The mathematical understanding of tilings and patterns is relatively poor even today.
- It is essentially a unexplored area.
- The mathematical analysis of weavings is almost completely untouched. (Weaving, as the mathematical content of Celtic knots and Islamic patterns. It can be considered topologically as knots and braids, or as certain uniform lattice network with marked nodes and edges with a geometric layout.)

- Penrose tiling is a aperiodic tiling.
- The discovery of Penrose tiling was a break-thru in mathematics and crystallography with great ramifications (For example, material science).
- The beauty of aperiodic tilings is that their orderliness is subtle.
- Such type of beauty was not possible in the past.
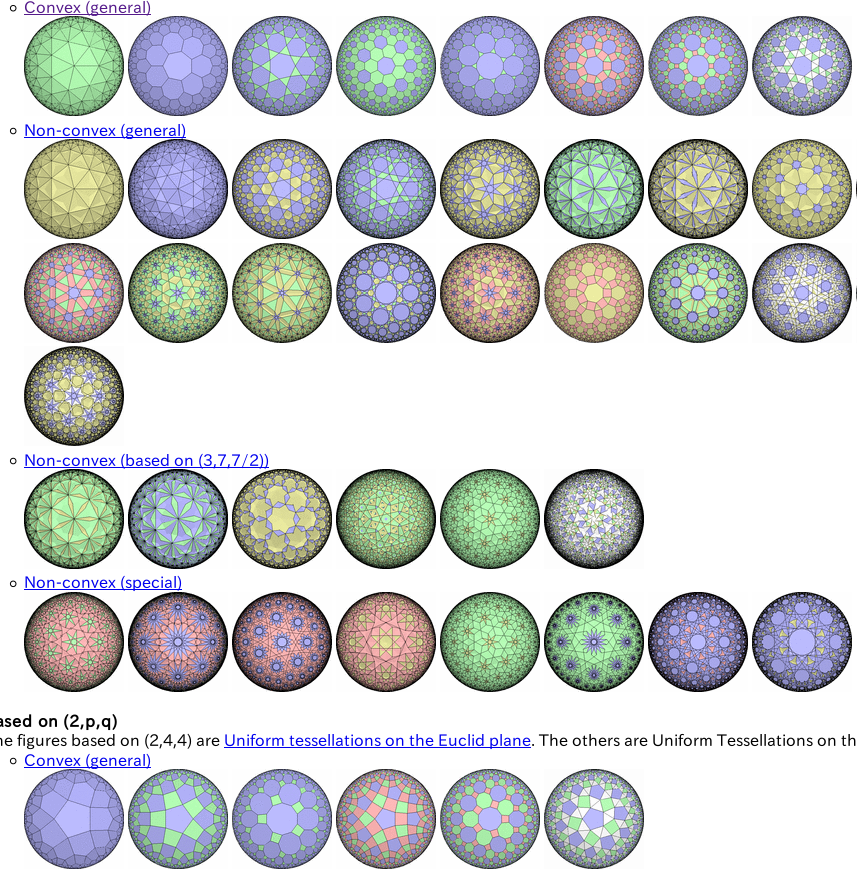
- Mandara: The World of Uniform Tessellations
- By hsaka.
- http://www2u.biglobe.ne.jp/~hsaka/mandara/index.html
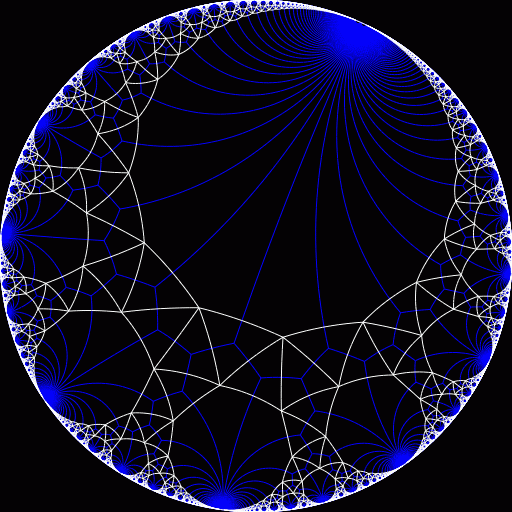
Modern math knowledge adds incredible amount of new possibilities at decorative designs. The math understanding of symmetry, and the discovery of aperiodic tilings, and also designs based on hyperbolic geometry, were all not possible before.
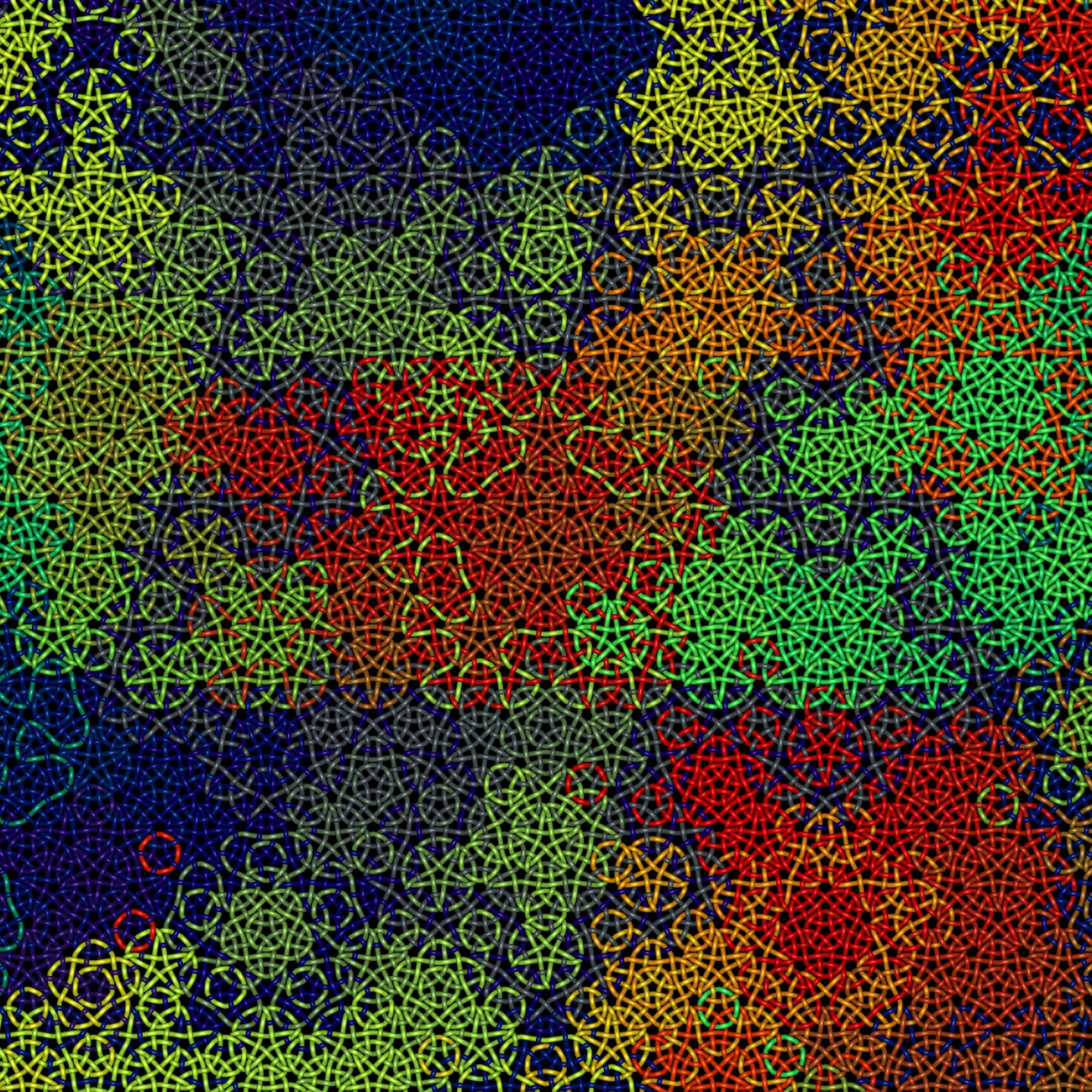
More example of tilings:
-
- Islamic Star Patterns
- By Craig S Kaplan.
- https://cs.uwaterloo.ca/~csk/other/starpatterns/
-
- Mitre System tilings
- By Ed Pegg Jr.
- http://www.mathpuzzle.com/Mitre2.html
- Xah Lee, a gallery of 17 possible symmetries based on a single penta-star motif. Wallpaper Gallery
- Xah Lee's photos of Aladdin hotel resort in Las Vegas, has many traditional Islamic styled architecture and indoor decorations.
- Dror Bar-Natan's Image Gallery, has photos of diverse artifacts showing each and every plane symmetries. @ http://www.math.toronto.edu/~drorbn/Gallery/Symmetry/Tilings/index.html
Fractals, IFS


Fractals are plots of mathematical objects. They began as a visual aid of a mathematical process. Essentially, each point in the plane is colored according to how that value (x,y) behaves when fed into a formula recursively.
Fractals, by its very nature of garishness and bizarreness, has been extremely popular among computer artists — even those who are not interested in mathematics or computer science. Fractals as a visual art have been explored extensively, and great many varieties and galleries have been created on the web.
The exploration of fractals as a visual art form has somewhat limited expression. Artistic creativity is limited to concocting equations and coloring schemes. Some people have started to mix computer generated fractals with manual manipulations, such as mixing in digitally modified photos. Such artwork ceases being algorithmic or mathematical.
Higher Dimensions
As we understand higher dimensional spaces, it opens a great gate of algorithmic art thru the process of projection or slicing of higher dimensional objects to 3-dimensional space or the plane.
Non-Euclidean geometry and higher dimensional geometry and topology are understood by only a few mathematicians in the world. (perhaps a few thousand people, or less if we are specific in the field) Consequently, artistic exploits thru their understanding are basically non-existent. Almost all ideas discussed in this page can be thought about in higher dimensions and or non-Euclidean space. In higher dimensions, there are totally new concepts that are non-existent in lower dimensions. (orientability, embedding, isotropism, etc) As math and technology march on, we may see more visual art explorations thru higher dimensions.
As a example, one idea of creating tilings and patterns is to slice thru some regular lattices of some higher-dimensional manifold. And, we may ask whether it is possible to encode some higher-dimensional manifold properties (such as orientability or the geometry it admits) by a visual exhibition. (i do not quite understand this, but for example, we can illustrate the angle-invariant property of inversion by showing the before and after images of a rectangular grid. We can also show linear and affine transformations by the way they look when applied to a grid. We can show properties of projective transformation and Conic Sections by shadowing. (think of beautiful stained glass in great Cathedrals) We can show homeomorphism or continuous transformation by animation, especially on tilings. We can color surfaces by their curvature, and draw gridlines along constant curvature lines, and show invariance of curvature such as the helicoid-catenoid surface family.

M C Escher
M C Escher (1898 to 1972) is a Dutch artist whose works are predominated by mathematical themes, many of which are purely algorithmic. Although, Escher is a traditional artist; his algorithmic arts are done manually, not by a program from computer, nor with a explicit algorithmic specification.
It is easy to go from algorithms to visual images, but given a algorithmic artwork, it is difficult to extract the algorithm in the form of a precise runnable program. The following two works by M C Escher illustrates this:

- butterfly, by M C Escher is clearly purely algorithmic.
- However, it is not trivial to extract the algorithm involved and turn it into a working program.
- From a pure minimalist point of view, one should be able to start with half a image of a butterfly, and apply a algorithm recursively to get the final image.
- Note that the butterfly's wings are colored in such a way that mutually orthogonal circles are formed, and this must be encoded in some way into the algorithm.
- There are different algorithmic approaches.
- One can do it by describing pen paths as in Turtle Graphics, or by recursive replacement as in L-Systems.
- Perhaps a least interesting way is by a mapping process with some mathematical model such as hyperbolic geometry on a rotational-symmetric tiling.
- Once a algorithm is obtained, one should be able to apply it to various motifs, or tweak parameters to get different effects.

- Whirlpools, by M C Escher is also clearly algorithmic.
- It consists of a strip of a repeated motif (the fish), wrapped into a double spiral.
- To generate this image algorithmically, one can start with a motif, reflect and glide-reflect to get a long strip, then use a function that map the strip into a spiral, then mirror to get the other spiral.
- (or use a function that maps a strip into such double-spirals) Finding the function may not be easy.
- I imagine to get it right it might take several days tweaking it with functional programing languages such as Mathematica, Lisp, Haskell.
- Perhaps a more elegant but even more difficult approach is to describe it recursively, which would also deal better with singularities at the center of each spiral.

- Escher's metamorphosis.
- This theme of aglorithmtically transforming a tiling is particular type of algorithmic mathematical art.
- It has been studied notably by Douglas Hofstadter.

- Snakes, by M C Escher is Another algorithmic mathematica art.
- This artwork is made by inter-linked circles of various sizes to form a weaving, in a specific geometric layout inside a circle.
- The snake animal drawings are mere decorations that adds spice to the artwork.
- To generate this work algorithmically, one needs to encode the knot process. (i.e. when there is a intersection between 2 circles, which one goes on top.).
- One also needs to encode the geometric layout, namely, the circle's positions and sizes.
- Note that circles are smallers near the center, but also gets smaller near the edge.
- This size change is not linear.
- Also, note that the circles have 3 different colors.
- The coloring basically cycle thru as they are spread toward the edge.
- Also, each of the circle ring has a slant (a thin side), either facing the center or facing the edge.
(M C Escher's artworks are copyrighted by M.C. Escher Company B.V.)
What is Algorithmic Mathematical Art
A visual artwork is mathematical if:
- The graphics encodes a non-trivial mathematical structure in a visual way. i.e. it is recursive, or symmetric, or embodies a mathematical equation.
Algorithmic Artwork
A visual artwork is algorithmic if:
- The source code is written in a way that reflect the structure. For example, raytracing code is not algorithmic, nor manually hardcoded list of coordinate points of solutions to a 3D surface.
The Algorithm in Algorithmic Mathematical Artwork
- Algorithmic artwork might not be generated by a computer program.
- M C Escher's artwork are examples of algorithmic artwork not generated by computer programs.
- Computer generated algorithmic artworks might not be generated algorithmically either.
- Here, “algorithmically generated” means a program that distills the inherent algorithmic nature in a artwork.
- For example, many tilings and patterns artwork today are spitted out by computer programs, but the programs are written in a ad hoc, case-by-case basis, consisting of drawing commands tweaked to match a desired output.
- Although generated by a program, but the essence of creation is manual.
- What we really want are programs in a form that embody, capture, or distill the algorithmic nature of the artwork, as a executable specification by means of recursion or symmetry code.
- The beauty of algorithmic artwork lies in its inherent beauty of algorithmic pattern or symmetry, and its creation process should be done that way.
- When this is achieved, and its algorithmic essence is captured, and we can then create vast numbers of variations by changing parameters or input.
- (This does not imply that results will be similar, as we know from chaos theory.).
- Generating a algorithmic mathematical art by a algorithmic process can be likened to specifying a Sequence by Recursion , or a group by generators and relations , or modeling a physical phenomen by a equation or cellular automata.
- It is a pursuit of elegance that captures essence, and gives us a precise insight on relations.
Example of Not Algorithmic Mathematical Art
Generative Art
So-called generative art are not mathematical art considered here, because they lack mathematical structure.
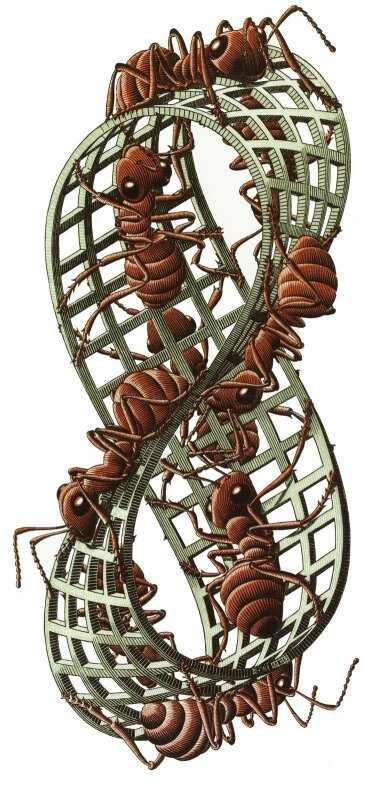
Math-based Art
some Escher's art are works of art illustrating mathematical ideas, but not the mathematical art discussed here.

Ray-Traced Computer Graphics
- Artwork generated by computer programs are not necessarily algorithmic.
- Ray-traced computer generated sceneries, or digitally retouched fractal artworks, are not considered algorithmic, in our context.

Evolutionary Programing and Cellular Automata
Evolutionary programing is a emerging method to generate visual art. The method is often done as genetic programing with human arbiter for judging the survival of the fittest. However, most of the investigations done so far over the 1990s tend to be insults to eye with the excuse of being abstract “art”. They are not mathematical.

- Cellular Automata (CA) methods can also be used for mathematical visual art.
- Stephen Wolfram's book A New Kind of Science contains many pleasing images of cellular automata, although not for the express purpose of visual art.
- For example, it is frequently cited that the patterns on sea shells are results of cellular automata. This is a example of using CA for non-mathematical art. (That is, the image does not contain some inherent math structure or appeal.).
- However, CA probably can be exploited for mathematical art.

- For example, consider the great varieties of seashell shapes. (See: Math of Seashell Shapes) Some has horns, spikes, ribs.
- Some are long, some are flat, and there are many types of overall spiraling structure.
- Seashells are grown from the calcium deposits secreted by the mollusks, and over the years many different shapes emerged thru evolution.
- Therefore, it is conceivable that a 3-D cellular automata can be set up with genetic programing to simulate the evolutionary process, as to obtain the many shapes of seashells as pure art of mathematical spiraling surfaces.
- 〔GeoMorph (~2002) by Harry Foundalis. (Generating surfaces with genetic programing element and manual evaluation). @ http://www.foundalis.com/mat/geo/geomorph.htm〕
Related Websites and References
Here are some list of people i know who are doing algorithmic art, mathematical art, or whose artwork are heavily math related:
- Michael Trott has been exploring mathematical art with Mathematica since early 1990s. His works are published in Graphica coffee-table book and a 4-volumes set of books titled Mathematica Guidebook Buy at amazon, 2005. Samples of his artwork can be found at: http://www.graphica.com/gallery/, http://www.mathematicaguidebooks.org/gallery/
- Sandor Kabai has created many fantastic algorithmic mathematical art. He is one of the most productive on the subject. His gallery is at: http://www.kabai.hu/
- Russell Towle. He does mostly polytope and zonotope studies of higher dimensions: polytope, zonohedra.
- Hop David. A traditional artist who does many creative mathematical illustrations. http://clowder.net/hop/index.html
- Craig S Kaplan. A computational geometry specialist, who did many artwork in tiling and patterns: https://cs.uwaterloo.ca/~csk/publications/
- Douglas Hofstadter. He is most famous for his Gödel, Escher, Bach Buy at amazon book. He has long been interested in AI and its relation to art. He has published article in Scientific American on Parquet Deformations. That is, the gradual transformation from one tilings to another in a strip. I don't know if he has done much artwork per se as discussed here.
- Ed Pegg Jr's, a recreational mathematician. Creator of the site mathpuzzle.com. The site contains a huge amount of high-quality mathematical illustrations. However, most of them are not done programmatically. Most of them are simple illustrations, but some are artistic. For example, his “Mitre System” tilings: http://www.mathpuzzle.com/Mitre2.html
The following is a annotated list of books that have influenced my outlook one way or another.
- Tiling and Patterns By B Grunbaum and G C Shephard. Buy at amazon The most authoritive and informative opus on the subject. Special thanks to professor B Grunbaum for sending me his various publications on the subject.
- A New Kind Of Science By Stephen Wolfram. Buy at amazon Aspects on Cellular Automata and its beauty.
- The Algorithmic Beauty of Sea Shells By Hans Meinhardt, Przemyslaw Prusinkiewicz, Deborah R Fowler. Buy at amazon There is also a similar book on plants.
- Visions of Symmetry By Doris Schattschneider. Buy at amazon A coffee-table book of M C Escher's tiling work. Most beautiful.
Books on Islamic geometric patterns.
- Islamic Art and Architecture from Isfahan to Taj Mahal By Thames and Hudson. Buy at amazon
- The Art of Islam (UNESCO Collection of Representative Works: Art Album Series) (1992) By Nurhan Atasoy, Afif Bahnassi, Michael Rogers. (ISBN: 2080135104) Buy at amazon Excellent, squarish large book. Mostly just photos with captions. Covers mostly architectures, and wall decorations.
- Splendors of Islam “Architecture, Decorations and design” (2000) By Dominique Clevenot and Gerard Degeorge. Buy at amazon Coffee-table book. Contains the most beautiful photos of Islamic architecture and decorations.
- The Art and Architecture of Islam 1250 to 1800 By by Sheila S Blair, Jonathan M Bloom. Buy at amazon Largish Coffee-table book. Lots of text with lots of photos.
- Islamic arts By by Sheila S Blair, Jonathan M Bloom. Not a coffee-table book. Scholarly book, with mainly text with excellent photo or image about other page. Color all types of artifacts. Very good.
- Symmetries of Islamic Geometrical Patterns By Syed Jan Abas, Amer Shaker Salman. Buy at amazon Contains black and white drawings of about 250 Islamic wallpaper patterns. Perhaps the most complete collection in print. The author Syed Jan Abas has a home page at: http://www.bangor.ac.uk/~mas009/islampat.htm.
Math and Illustrations
- Algorithmic Mathematical Art
- Art of M C Escher
- Escher Chameleon Polyhedron
- What is Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra
- Outline Rendering of 3D Models
- Autostereogram
- Visual Illusions
- Projective Illusion
- What Is Perspective Drawing
- Illustrating Geometry with POV-Ray