Xah Talk Show 2025-11-04 Ep709 Wolfram Language Coding and Tutorial, List Operation. Emacs Workflow.

• https://youtu.be/8cf4R_0bSTQ

• Wolfram Language for Programers
• Wolfram: Download Wolfram Engine

• Wolfram: List Operations
• Wolfram: List. Join, Union, Intersection, Difference
• Wolfram: List. Create (Table)
• Wolfram: Create Flat List (Range)

• Emacs: Xah Wolfram Mode 📦

• Rainer Joswig (aka lispm) Libel Xah Lee, on Hackernews

• Emacs Flaw: Texinfo Should be HTML (2009)

• Xah Lee is a prominent figure known for his extensive online resources on Emacs and programming, including discussions on the Texinfo documentation system.
• He has expressed criticism regarding Texinfo, advocating for the adoption of HTML as a replacement for Texinfo in Emacs documentation.
• Lee argues that the current Texinfo format, which uses a syntax like (info "(viper) Top"), is poorly understood by most programmers and hinders the accessibility and spread of Emacs documentation.
• He believes that adopting HTML would make documentation more universally accessible, as URLs are more intuitive and clickable than Lisp expressions, thereby improving user engagement and understanding.

• Texinfo, the system used for generating both online and printed documentation, was created by Richard M.
• Stallman and is the official documentation system for the GNU Project.
• It allows a single source file to be converted into multiple formats, including Info, HTML, PDF, and DVI, using tools like texi2any.
• The format is designed to support structured documents with chapters, sections, cross-references, and indices, and is implemented as free software under the GNU General Public License.
• Despite its capabilities, Lee and others have pointed out that Texinfo's output formats, such as Info, are less user-friendly compared to modern web standards like HTML.

• Lee has also highlighted issues with Texinfo's integration with modern web technologies, noting that while HTML is the standard for web documentation, Texinfo remains entrenched in the GNU ecosystem.
• He has suggested that Emacs could benefit from integrating HTML rendering directly, potentially using a built-in parser or borrowing from existing rendering engines like Firefox, to improve performance and usability.
• His advocacy reflects a broader call for modernization within the Emacs and GNU communities to align with contemporary web standards and improve user experience.

• AI-generated answer.
• Please verify critical facts.

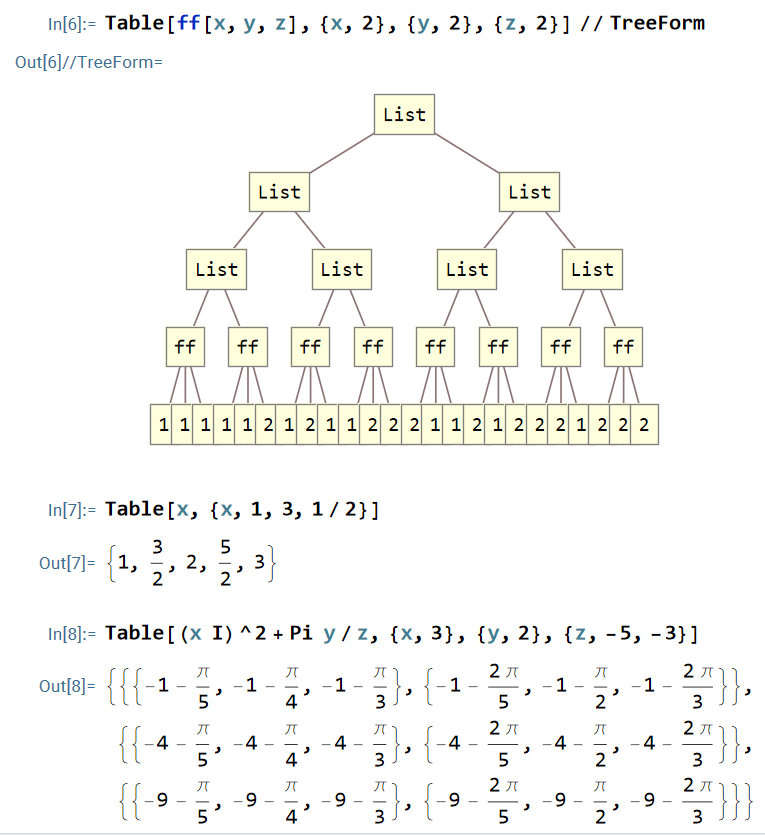
Table[ x, 3]
(* {x, x, x} *)

Table[ 2, 3]
(* {2, 2, 2} *)

Table[ x, {x, 3}]
(* {1, 2, 3} *)

Table[ x, {x, 4, 7}]
(* {4, 5, 6, 7} *)

Table[ x Pi , {x, 4, 7}]
(* {4*Pi, 5*Pi, 6*Pi, 7*Pi} *)

Table[ x^2 , {x, 4, 7}]
(* {16, 25, 36, 49} *)

Table[ x^2 + y , {x, 4, 7}]
(* {16 + y, 25 + y, 36 + y, 49 + y} *)

Table[ {x^2 + y, x y+z} , {x, 4, 7}]
(* {
{16 + y, 4*y + z},
{25 + y, 5*y + z},
{36 + y, 6*y + z},
{49 + y, 7*y + z}} *)

(* HHHH------------------------------ *)

(* 2 dimensional examples *)

Table[ f[x,y], {x, 3}, {y, 2}]
(* 
{
{f[1, 1], f[1, 2]},
{f[2, 1], f[2, 2]},
{f[3, 1], f[3, 2]}
} *)

Table[ x I + Pi y, {x, 3}, {y, 2}]
(* {{I + Pi, I + 2*Pi}, {2*I + Pi, 2*I + 2*Pi}, {3*I + Pi, 3*I + 2*Pi}} *)

Table[ (x I)^2 + Pi y/z, {x, 3}, {y, 2}, {z, -5,-3}]

(* {{{-1 - Pi/5, -1 - Pi/4, -1 - Pi/3}, {-1 - (2*Pi)/5, -1 - Pi/2, -1 - (2*Pi)/3}}, {{-4 - Pi/5, -4 - Pi/4, -4 - Pi/3}, {-4 - (2*Pi)/5, -4 - Pi/2, -4 - (2*Pi)/3}}, {{-9 - Pi/5, -9 - Pi/4, -9 - Pi/3}, {-9 - (2*Pi)/5, -9 - Pi/2, -9 - (2*Pi)/3}}} *)